Vieta Jumping and Problem 6 | Animated Proof
IMO 1988 Problem #6 - using Vieta's Formula and Fermat's Method of Infinite Descent 108Подробнее

Prove Method of infinite Descent (Vieta's jumping) : (a^2+b^2)/(ab+1) is square, imo1988Подробнее

Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988Подробнее
You, Me and The Legend of Question 6Подробнее

The Return of the Legend of Question Six - NumberphileПодробнее

What is the algebraic intuition behind Vieta jumping in IMO1988 Problem 6? (7 Solutions!!)Подробнее

The hardest problem on the hardest testПодробнее

Vieta Jumping explainedПодробнее
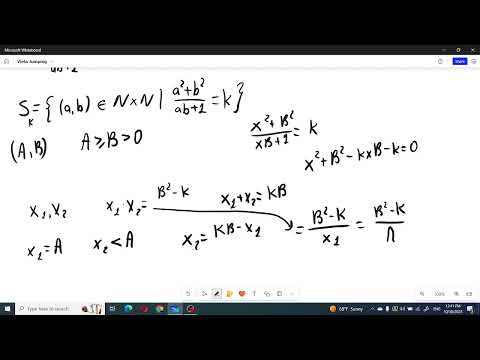
Chinese IMO teamПодробнее

The Notorious Question Six (cracked by Induction) - NumberphileПодробнее

Prove Method of infinite Descent (Vieta's jumping) : (4a^2-1)^2/(4ab-1) is integer, then a=bПодробнее
Prove Method of infinite Descent (Vieta's jumping) : (x^2+y^2+1)/xy=3Подробнее

BMO2 2013 Q1 - Vieta JumpingПодробнее
